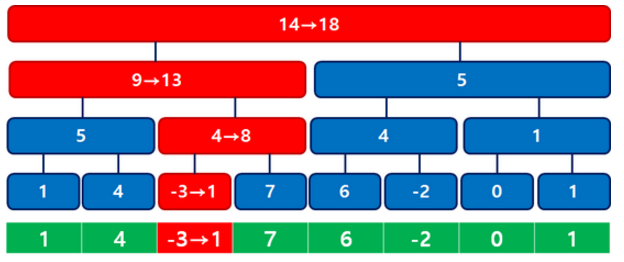
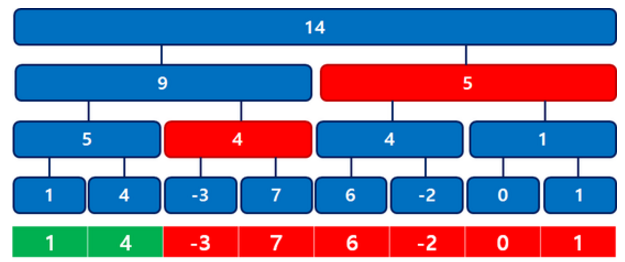
Segment Tree (구간 트리)

트리의 노드들이 범위를 나타내는 경우 이를 세그먼트 트리 라고 한다.

N개의 공간이 있을때, 전체 구간을 [0, N-1] 이라고 하면

리프 노드들은 길이가 1인 각각의 구간을 가지고 있고, 부모 노드는 자식들의 구간의 합을 갖고 있으며, 모든 구간은 연속적이여야만 한다.

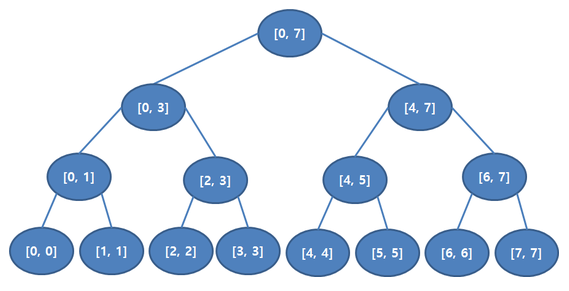
위의 그림은 0~7 까지의 아이템을 세그먼트 트리로 나타낸 것이다.

트리의 노드가 구간 정보를 가지고 있다.

세그먼트 트리의 크기를 계산

문제에서 주어진 아이템이 2^H 형태 이면, 세그먼트 트리의 크기는 2^(H+1) -1 이다.

H는 세그먼트 트리의 Depth(Height)가 된다.

• 아이템이 4개 이면 2^2 형태 이고, H = 2
• 2^(H+1) -1 = 2^(2+1) - 1 = 2^3 -1 = 7

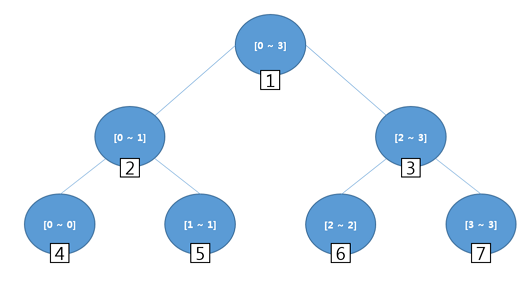
• 만약 2^H 형태가 아닌경우 가장 근접한 H를 찾는다
• 아이템이 9개 이면, 2^3 + 1 이고 가장 근접한 H = 4 가 된다.

따라서, H = log2(N)

세그먼트 트리의 크기는 2^(H+1) -1 로 구할 수 있다

// log2(N) 함수
public static int log2(int x) {
    Double result = Math.log(x) / Math.log(2);

    return result.ceil(result); // 무조건 올림 매서드 호출
}

// 트리 크기 구하기 및 트리 초기화
public static void initTree() {
    Double len = Math.pow(2, log2(ItemNumber) + 1) - 1;

    tree = new int[len.intValue()];
}

// 2^H 형태로 구하기 않고 4를 곱해서 크기 계산 (메모리 낭비가 있음)
public static void initTree() {
    tree = new int[ItemNumber * 4];
}

세그먼트 트리를 생성

트리노드가 leaf 이면 자기 값을 트리에 저장하고,

leaf가 아니면 왼쪽, 오른쪽 노드 값을 계산하고 저장하는 형태로 생성한다.

public static int createTree(int nodeId, int L, int R) {
    // leaf 노드
    if (L == R) {
        tree[nodeId] = itemList[L];
        return tree[nodeId];
    } else {
        // leaf 노드가 아니면
        int mid = (L + R) / 2;
        int leftTreeSum = createTree(nodeId * 2, L, mid);
        int rightTreeSum = createTree(nodeId * 2 + 1, mid + 1, R);

        tree[nodeId] = leftTreeSum + rightTreeSum;

        return tree[nodeId];
    }
}

create(1, 0, N-1);

세그먼트 트리 검색

세크먼트 트리를 방문하는 함수

• 구하려는 구간 L, R
• 세그먼트 트리의 노드 ID (index), 이미 트리에 해당 ID에 값이 있으면 그 값을 리턴
• 노드 구간의 시작을 nodeL, 구간의 끝을 nodeR

public static int query(int L, int R, int nodeId, int nodeL, int nodeR) {
    // 구하려는 범위가 노드의 범위를 벗어나는 경우
    if (L > nodeR || nodeL > R) {
        return 0;
    }

    // 구하려는 범위가 노드의 범위를 포함하는 경우
    if (L <= nodeL && nodeR <= R) {
        return tree[nodeId];
    }

    // 그 이외의 경우
    int mid = (nodeL + nodeR) / 2;
    int sumL = query(L, R, nodeId * 2, nodeL, mid);
    int sumR = query(L, R, nodeId * 2 + 1, mid + 1, nodeR);

    return sumL + sumR;
}

public int query(int left, int right) {
    return query(left, right, 1, 0, N-1);
}

query(0, N-1);

[2, 7] 범위의 합을 구하는 예제

세그먼트 트리 갱신

세그먼트 트리의 노드 데이터가 변경되는 경우, 세그먼트 트리를 업데이트하는 함수

public static void update(int nodeId, int nodeL, int nodeR, int itemIndex, int itemValueDiff) {
    // 변경하려는 노드의 인덱스가 노드의 범위를 벗어나는 경우
    if (itemIndex < nodeL || itemIndex > nodeR) {
        return;
    } else {
        // 변경하려는 노드의 인덱스가 노드에 포함되면
        tree[nodeId] += itemValueDiff;

        // leaf 노드가 아니면 자식노드의 왼쪽, 오른쪽 갱신
        if (nodeL != nodeR) {
            int mid = (nodeL + nodeR) / 2;
            update(node * 2, nodeL, mid, itemIdex, itemValueDiff);
            update(node * 2 + 1, mid + 1, nodeR, itemIndex, itemVauleDiff);
        }
    }
}